Abstract

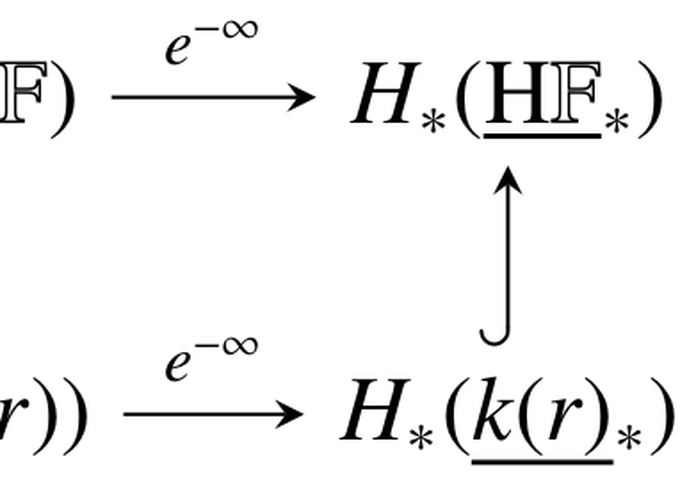
This paper examines the mod 2 homology of the spaces in the Omega-spectrum for connective Morava $K$-theory, i.e., the mod 2 Hopf ring for connective Morava K-theory. A natural set of generators for this Hopf ring arising from the homology and homotopy of the connective Morava K-theory spectrum is calculated and the non-trivial circle product relations among the generators arising from homology and homotopy are determined. This Hopf ring calculation is accomplished using Dieudonné ring theory and Adams spectral sequences for the connective Morava K-theory of Brown–Gitler spectra.

Paul Pearson

Associate Professor of Mathematics

My research interests include algebraic topology, applied mathematics, and machine learning.